〈問題〉
●カップの中にボールはいくつ入りますか?
●ボールの大きさとカップの大きさの数値とその関係は?
●世界のトップ・プロ(天才・名人・達人)たちの距離に対するカップ・インの確率は何%ですか?

ボールを真っすぐコロがすためのインパクトに必要な3条件
条件1
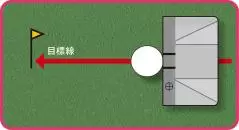
目標線に対してリーディングエッジがスクエアであること
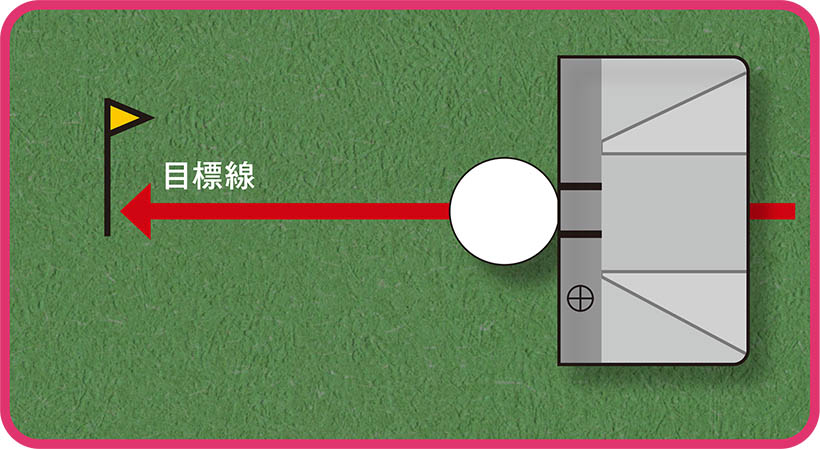
条件2
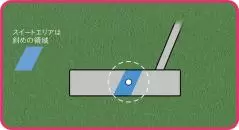
フェース面上のスイートエリアとボールの中心が一致すること
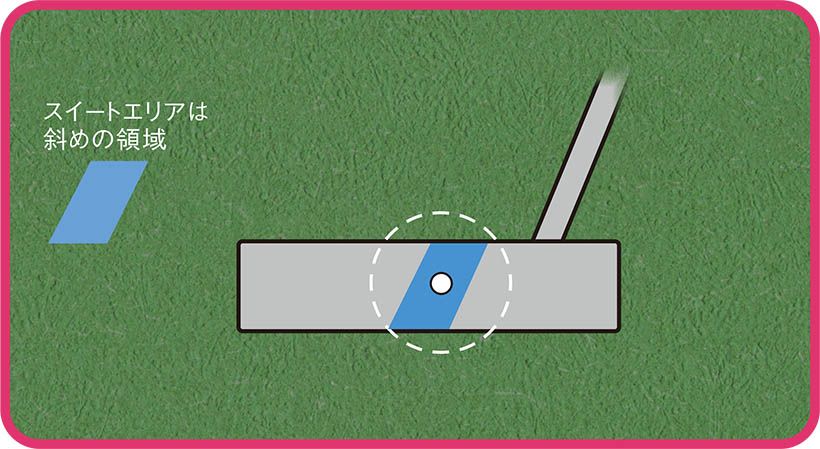
条件3
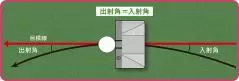
パターヘッドが目標線に対して均等なインサイドインを形成すること
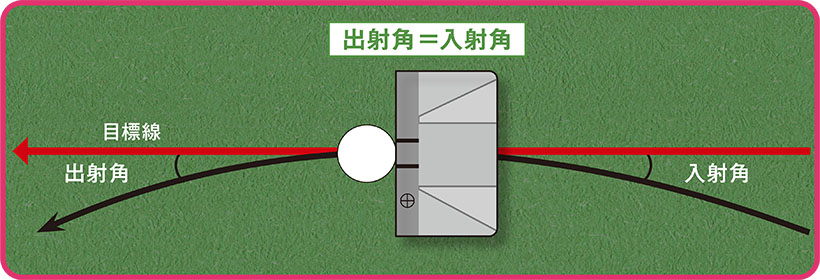
技術で悩む前にまずは敵を知る
清永 これまでパッティングに関する多くのことを一緒に学んできました。そこで、ふと思ったのですが、基本的なことは理解されていますでしょうが?
GT といいますと?(汗)
清永 カップの直径は何センチでしょう?
GT ……。
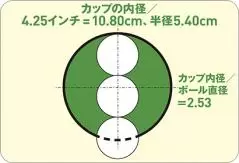
清永 4.25インチ、センチに直すと10.80㎝! ではボールの直径は?
GT ……。
清永 1.68インチ、センチに直すと4.267㎝! やはり不安が的中しましたね。ゴルフメディアとしては、このくらいのことは頭に入っていてスラスラ答えてもらわないと困りますね! では、これらのことを踏まえてボールはカップに何個入りますか?
GT 2.5個……。
清永 はい正解、2.53個ですね。計算上は、ど真ん中に入らないとしても4月号で記したように中心から(カップの半径)―(ボールの半径):5.4ー2.134=3.27㎝の2倍となる6.54㎝外れてもカップインするということになります。では質問を変えましょう。名手がパッティングするとして距離1mに対してカップインする確率はどのくらいでしょう?
GT 1mですよね? そりゃ、トッププロですから100%に近いのではないでしょうか?
清永 だいたい当たっています。それでも90%と言っていいと思います。では2mは?
GT 2mでしょう? 1発で入ればうれしいけれど、まあまあ離れていますよね。30%くらいとか?
清永 そうですね50%くらいかと思われます。では3mは?
GT 今度こそ30%……?
清永 やっと正解ですね。感覚的に答えられていると思いますが、ここで何か気づきませんか?
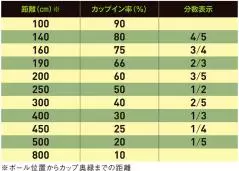
GT 1mが90%、2mが60%、3mが40%だから3分の1強。あっ、だいたいメートル分の1ということですか!?
清永 気づきましたね! トッププロがこのくらいですので一般のゴルファーはちょうど距離で割った確率でカップインすると考えてもらえばいいのです。
GT 当たりましたね! でもそんなもんですか? 2mとかもっと入ってもよさそうに思いますが。
清永 トッププロでさえそんなものです。それなのにアマチュアのみなさんは長い距離でも1パットで入れようとする。3mくらいでも1パットで決めてやると、アドレスから力んでいる姿をよくお見受けします。
GT 3mくらいまでは狙いにいって、外れてすごく悔やんでいる気がします。とくに2mくらいのパットを外すと残念ですし入れてやろうっていう気持ち、外したら恥ずかしいと思う気持ち。プロでさえそのくらいの確率だと知れば、もし入らなくてもメンタル的にもラクですよ。
清永 その通りです。上手い人でさえそんな確率なのです。これを知ると気もラク、イップスも離れていくというものです。
みなさん知っていますか?
ボールとカップの大きさの関係
-
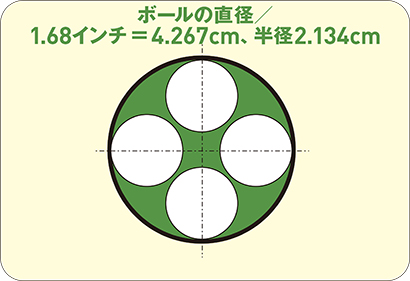
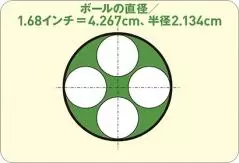
ルールで決められているボールの直径は4.267cm。カップの大きさに敷き詰めると上図のようなイメージ。
-
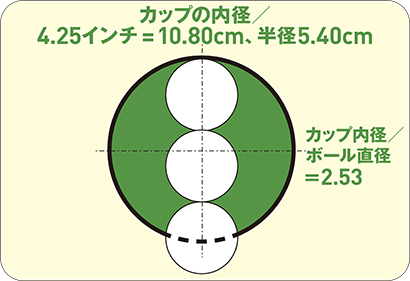
カップの内径は10.80cmで半径は5.4cm。ボールを中に敷き詰めると上図のようなイメージ。
パット名人が打った場合の距離とカップインの確率
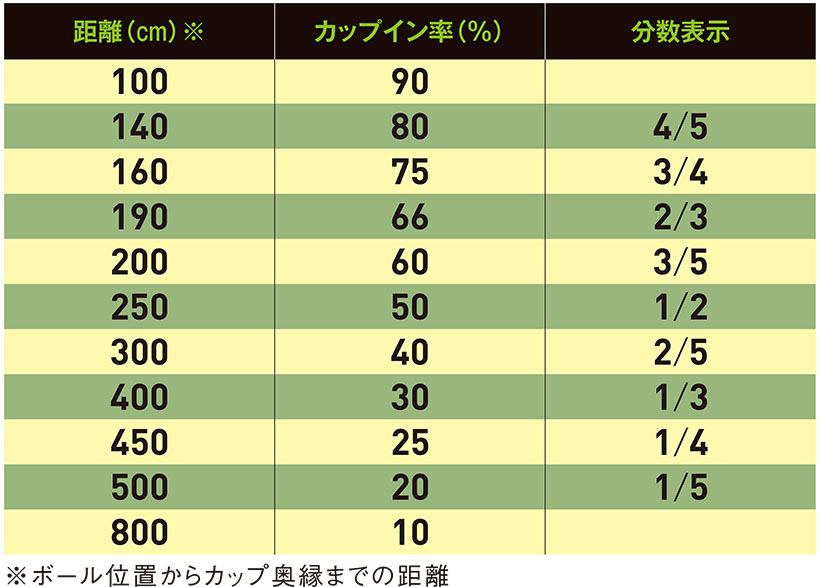


解説/清永 明
福岡大学名誉教授。大学時代は九州学生選手権を3連覇。医師でありながらゴルフにまつわる現象を物理の目で分析。1メートルのパットが90%の確率で入るヨネックスの「トライプリンシプルパター」の設計者としても有名。