真っすぐ向いているはずなのに!正しくフェースを合わせられない理由は“無意識(錯視・錯覚)の世界”にあった
カップインの第一条件。パターのフェース面は目標を向いていますか?|清永教授からの挑戦状 Vol.9
ゴルフの原理原則を疑い、分析した清永教授の常識を覆し、上達スピードが速まる理論を紹介!
ゴルフトゥデイ本誌 628号/130~131ページより
解説/清永 明
〈問題〉

パターのフェース面が目標に向いている確率は何パーセントでしょうか?
測定器を自作して確率を求めた
GT 先生は確か2010年8月にトライプリンシプルパターの創作を開始されて、2014年1月にヨネックスと契約。そこからパターの実証研究を開始されています。
清永 「ゴルファーは果たして静的な動作であるアドレス時にパターフェース面が正確に目標を向いているのか」を研究課題としました。
GT どのくらいズレているか確かめる方法はありますか?
清永 検証のために必要な器具として私は既存のパーツで自家製の「アドレス・チェッカー」なるモノを考案し作成しました。
GT 「アドレス・チェッカー」?
清永 金物を組み合わせたものですが、アドレスで構えてからフェース面に当てることでフェース面がどこに向いているかわかります。
GT これはわかりそうですね。
清永 この器具を使って、まずは私を実験台として数値を集めました。そうすると、ゴルフ歴40年の私、清永自身がアドレス時フェース面方向性に「錯視の存在」を自覚しました。
GT 先生も間違っていたと。
清永 はい。ちなみに私はどういうゴルファーか読者のみなさんに改めて紹介させて頂きます。
GT はい、お願いします。
清永 『50年間以上のゴルフ経験を持ち、かつ幾度かチャンピオンにもなり、それなりにパッティング技術を修得していたはず』なのです。
GT じゅうぶん「上手いゴルファー」のカテゴリーに入ります。
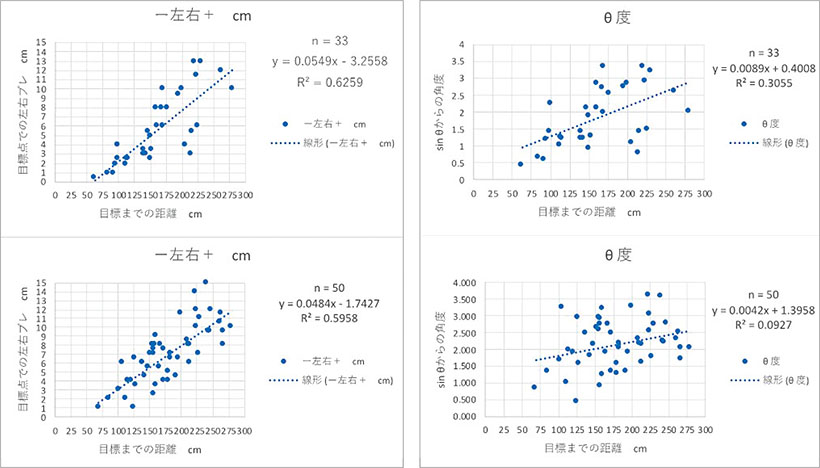
清永 それでもですよ、それでも「アドレス・チェッカー」を使って計測すると、アドレス時のパターフェース面の向きは1m前後で1~6cm右、2m前後では3~13cm右。つまり 常に狙い目の右側を向いていたという事実!
GT それでも左右にバラけることなく、安定して右を向いているじゃないですか!
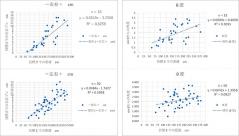
清永 そこはポイントではなく……。さらに「アドレス・チェッカー」を使ってデータを集計しましたら平均的には距離162.9cmで 5.7cm(181.2cmで7.0cm)右側を向いていました。つまり「2~3歩でカップ半分強右側」を向くと認識できたのです。
このとき初めて無意識(自分の錯視・錯覚)の世界を認識できたのです。試しにやってみますか?
GT ぜひお願いします!
清永 部屋で構いませんので、ほぼ平坦な場所で意中の目標物の1点を決めてください。パターのフェース面が「目標点に向いている認識」を持ち、かつ「己の眼力を確信」するに至ってからアドレスを解く。どうですか?
GT あっ……、全然違うところを向いています。
清永 そうなのです。真っすぐ向いているはずなのに、自分が思ってもいないところを向いているのです。
GT アドレスの向きでさえ、真っすぐ向けていないことがあるのに自分の手に持って、さらに離れているパターのフェース面を目標に向けるのは難しいということですよね。
清永 その通りです。ヒトの視覚に関しては大きな問題があります。この問題については養老孟司先生が「脳の見方」(筑摩書房)でわかりやすく説明されていますので、その一部分を引用し加筆させて貰います。『まずヒトの視覚には形に関する尺度依存性がないことを理解して下さい。ある物が網膜に写っているとき、網膜における像は自分と物との距離が近づけば大きくなり、遠ざかれば小さくなります。勿論視覚系は、そこで絶対的な大きさを問題にしてはならず、それらの像を「同じもの」として認識されなければなりません。これをもって「目の不完全性」と見なすこともできます。その不完全性のために、大きさを知ろうとすれば、現実には、われわれは、モノサシ(測定機器)を必要とするのです。』
見たことがあるかもしれませんが、面白い資料があるのでそれを示しておきますので、楽しみながら学んでください。
清永教授がフェース向きをチェックした実験方法
[1]部屋の平坦な場所で「意中の目標物の1点」を決める。
[2]パターフェース面で「アドレス・チェッカー」を小刻みに動かしながら、「目標点に向いている認識」を持ち、かつ「己の眼力を確信」するに至ってからアドレスを解く。
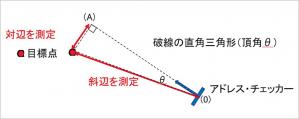
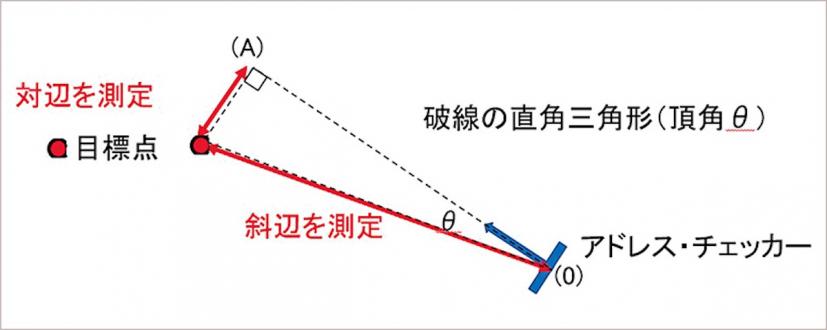
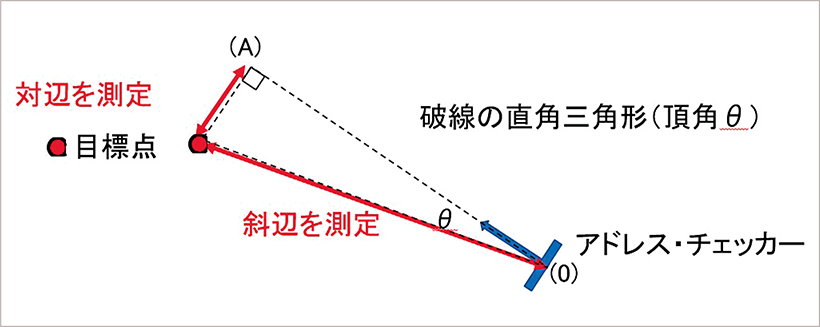
[3]測定は、アルミ製巻尺でアドレス・チェッカーのフェース面側の起点(0)から、矢印方向の延長する一点(A)までを正確に測定。単位は cm まで。下図に示すように、対辺に相当する距離と斜辺に相当する距離を測定。
[4]その際、目標点の左右のズレとなる対辺に相当する距離の表記は、左ズレの場合は「ー (マイナス)数値」とし、右ズレの場合を「+(プラス)数値」で表示すること。
[5]統計処理のためには必ず不作為とするために、目標点も1m前後から3m前後の距離までに一回毎に変えるだけでなく、方向も毎回毎に変える必要あり。
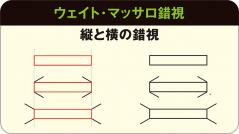
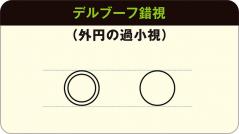
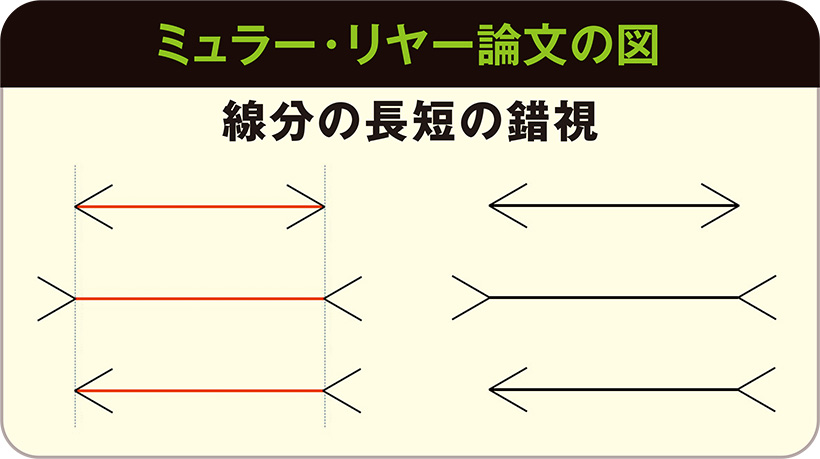
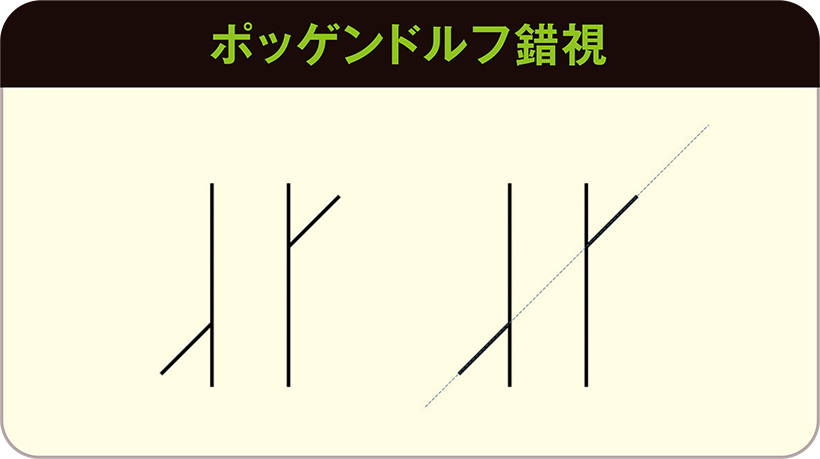
なんでこう見えるの? 錯覚と錯視の不思議
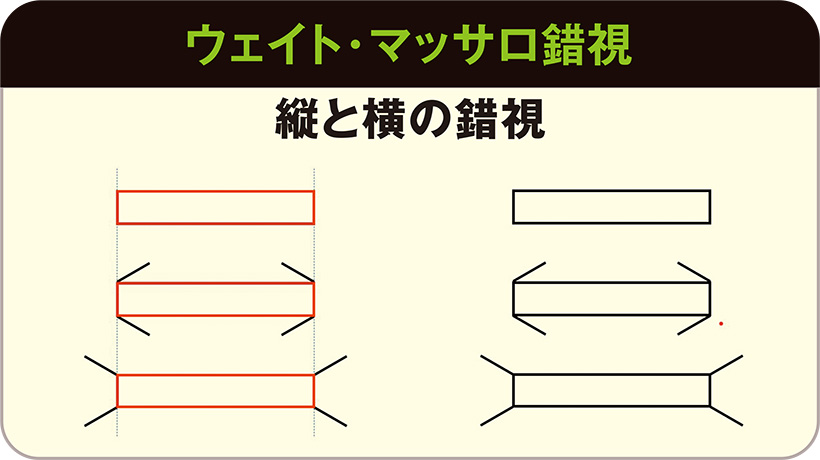
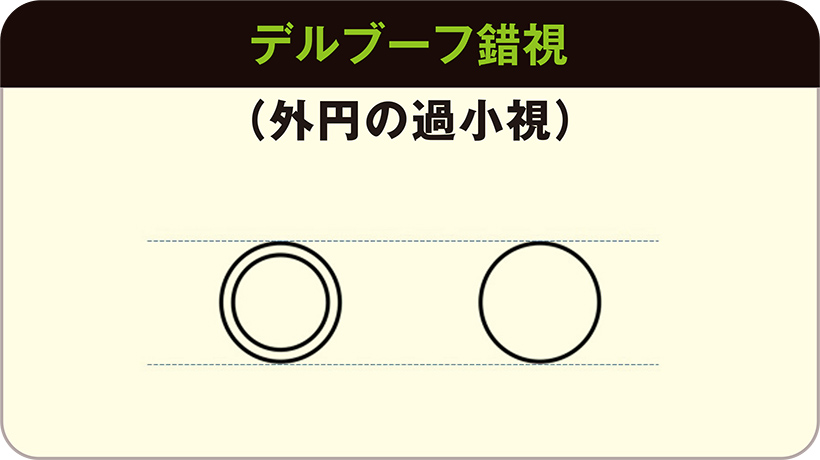

解説/清永 明
福岡大学名誉教授。大学時代は九州学生選手権を3連覇。医師でありながらゴルフにまつわる現象を物理の目で分析。1メートルのパットが90%の確率で入るヨネックスの「トライプリンシプルパター」の設計者としても有名。

ヘッドスピードを上げるには『連続素振り』が一番!【ゴルフ飛ばしてなんぼ!が出張レッスン!】
飛距離優先型のレッスンで定評の小池正次がレクチャーする「すぐに飛ばせるようになるコツ」シリーズ。第1回は飛ばしのスイン...

プロギア「PRGR 0 ウェッジ」球足を活かせる適度なスピンのピッチエンドランが打ちやすい!
プロギアからを2024年9月13日に発売された『PRGR 0 ウェッジ』をコースに持ち込んで、徹底的にレポートする。

カッコいい短パンの着こなし術を「日本シニアオープン」で聞いてみた!
先週の「日本シニアオープン」では本戦でも選手が短パンでプレーすることが認められた。 連日最高気温が30度を軽く超える暑...